This isn’t about theology, but I will talk about the number three.

We love the number three. Many of our rules/doctrines consist of three parts. For example, in Christianity, there is the theory of the Holy Trinity, stating that God manifests Himself in three forms: the Father, the Son, and the Holy Spirit. I’d love to cast them into a shamrock diagram:

The key idea here is that, although there are three forms, there is really only one God.

While I am not a Theologist, I appreciate the idea that an important concept is broken into three aspects, each of them stems from the same root, and connects with each other to promote deeper understanding of the subject. Let’s call them the “shamrock ideas”.

I happened to have encountered some of the interesting and beautiful shamrock ideas in the realm of science and mathematics. These ideas have given me incredible insights into subjects, helping me see the big pictures of a lot of seemingly scattered knowledge.

Science

Perhaps the most well-known example of a shamrock idea is the three components of science.

There are three great branches of modern science: theory, experiment, and computation.

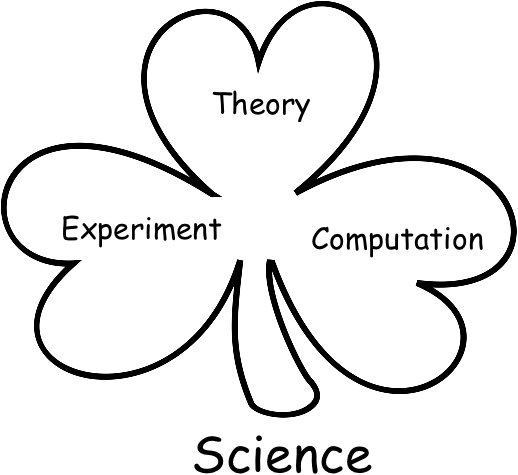
The keyword in this shamrock is computation, it reminds us how computation has influenced science, and has evolved from a mere tool into a full-fledged scientific branch.

In the early days of science, machines were invented to help scientists with their calculations. Searching the internet you will find calculators like Arithmometer (1850s-1910s) and Comptometer (1880s-1970s). Those machines can add, subtract, multiply and divide numbers. They were once very useful to scientists, and are now all gone to museums. In the mid-1900s, electronic computers started to take over, and computing power skyrocketed in the past 60 years. Computer performance evolved from hectoscale computing (~200 operations per second) with the first IBM computer in 1946, to petascale computing in 2009 with modern supercomputers, which is thousands of trillions of operations per second.

Such leap in computing power has unleashed ideas that were sheer impossible just decades ago.

With experiment, science have gone a long way tracing back to the ancient Greeks. With computation, science has taken off and is moving ever faster. We can simulate things that are too far (universe), too small (quantum), too expensive (medicine), or too complex (social network).

Mathematics

I would like to mention more shamrock ideas I found reading math.

Functions ¹

The function shamrock has three leaves respectively labeled formula, spectral coefficients, and grid point values. Together, these three concepts help us better understand and use functions. To see how these three concepts connect to each other, we realize that we go from the symbolic $f(x)$ to values ${f_j}$ by sampling, from $f(x)$ to spectral coefficients ${a_j}$ by integral transforms (e.g. Fourier transform), and from ${f_j}$ to ${a_j}$ by discrete algorithms (e.g. FFT).

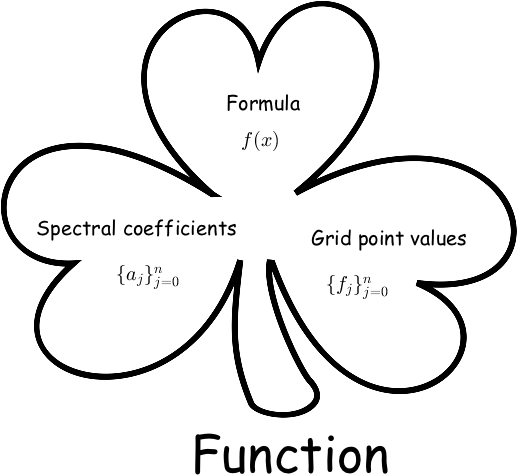
When solving a problem that involves a function $f(x)$, the symbolic formula is manipulated with analytical methods, its spectral coefficients are useful for Galerkin methods, and the grid point values are what the convenient pseudospectral methods operate on.

A mathematician would be crippled if failing to understand and to freely switch between any of them.

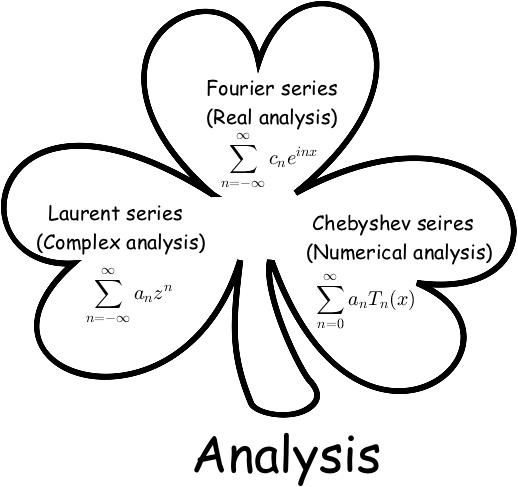
Analysis ²

This probably is my favorite shamrock. In analysis, the three types of series, Fourier, Laurent, and Chebyshev, are really the same series looking from different angles.

Let’s consider the substitutions

$$x = \frac{z+z^{-1}}{2} = \cos\theta$$

they give the equivalent relations

$$T_n(x) = \frac{z^n+z^{-n}}{2} = \cos(n\theta)$$

where $T_n(x)$ is the Chebyshev polynomial of order $n$. Given a smooth function $f(x)$ on $x\in[-1,1]$, it can be expanded as a Chebyshev series

$$f(x) = \sum^\infty_{n=0}a_nT_n(x)$$

which under the equivalent relations gives

$$\sum^\infty_{n=0}a_nT_n(x) = \sum^\infty_{n=0} a_n \frac{z^n+z^{-n}}{2} = \sum^\infty_{n=0} a_n \cos(n\theta)$$

or

$$\sum^\infty_{n=0}a_nT_n(x) = \frac{a_0}{2}+\frac{1}{2}\sum^\infty_{n=-\infty} a_{|n|} z^n = \frac{a_0}{2}+\frac{1}{2}\sum^\infty_{n=-\infty} a_{|n|} e^{in\theta}$$

The last equalities show the amazing relationships between the three branches of analysis, providing a picture about how viewing from different angles gives you different series expansions:

• If you look at the unit circle in the complex plane (or a periodic interval) $\theta\in[0,2\pi]$, you see Fourier series, the fundamental tool for real analysis
• If you look at the annulus $\frac{1}{\rho} < |z| < \rho$, you see Laurent series, the fundamental tool for complex analysis
• If you look at the interval $x\in[-1,1]$, you see Chebyshev series, the fundamental tool for numerical analysis

Such connections are always there, but you need to discover them. Even many math majors know little about the shamrock, and most of them have taken all three courses.

A final note

I love the shamrocks not because they teach me new concepts; in fact they don’t. I have understood the concepts in the three leaves of each shamrock before I saw them put together. The important thing of these shamrocks is that they provide a unified view, a new prospective that connects and sees things you knew differently. Like Kalid Azad (author of BetterExplained) once mentioned in a post, our understandings improve the most not when we’ve learned new concepts, but when mindset shifts happen.

References: